【TensorFlow】リカレントニューラルネットワーク(GRU)で為替レートを予測【FX】
- 2017.07.17
- Deep Learning Python TensorFlow
以前、リカレントニューラルネットワーク(LSTM)で為替レートの予測をしました。
今回は、LSTMをもう少しシンプルにしたGRUという方法を使って、同じようにレートの予測をしてみます。実装にはTensorFlowを使用します。
プログラム自体は以下のリンク先のコードを今回の目的に合わせて書き換えたものになっています。(私の好みで変数名を変えたりしています)
入力は1時間足の終値を10個、出力は、3時間後に上がるなら[1,0]、下がるなら[0,1]となります。
全データのうち、90%を学習用、残りの10%を評価用としています。
入力データの正規化に関しては、何が良いのか分からないので、適当に100を引いて、10で割っています。
プログラム
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 |
import numpy as np import tensorflow as tf from sklearn.utils import shuffle from sklearn.cross_validation import train_test_split import matplotlib.pyplot as plt def data_gen(x_len=25,shift=3): data=[] target=[] for i in range(0,len(input)-x_len-shift): data.append(input[i:i+x_len]) if input[i+x_len+shift]>data[i][x_len-1]: target.append([1,0]) else: target.append([0,1]) return data,target def inference(x,n_batch,x_len=None,n_hidden=None,n_out=None): def weight_variable(shape): initial=tf.random_normal(shape,stddev=0.1) return tf.Variable(initial) def bias_variable(shape): initial=tf.random_normal(shape,stddev=0.1) return tf.Variable(initial) cell=tf.contrib.rnn.GRUCell(n_hidden) initial_state=cell.zero_state(n_batch,tf.float32) state=initial_state outputs=[] with tf.variable_scope("RNN"): for t in range(x_len): if t>0: tf.get_variable_scope().reuse_variables() (cell_output,state)=cell(x[:,t,:],state) outputs.append(cell_output) output=outputs[-1] V=weight_variable([n_hidden,n_out]) c=bias_variable([n_out]) y=tf.nn.softmax(tf.matmul(output,V)+c) return y def loss(y,t): e=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y,labels=t)) return e def training(loss): train_step=tf.train.AdamOptimizer(learning_rate=0.0005,beta1=0.5).minimize(loss) return train_step input=(np.loadtxt("USDJPY60.csv",delimiter=",")-100)/10 x_len=10 shift=3 data,target=data_gen(x_len,shift) n_out=2 X=np.array(data).reshape(len(data),x_len,1) Y=np.array(target).reshape(len(data),n_out) N_train = int(len(data) * 0.9) N_validation = len(data) - N_train X_train, X_validation, Y_train, Y_validation = train_test_split(X, Y, test_size=N_validation) n_hidden = 32 x = tf.placeholder(tf.float32, shape=[None, x_len,1]) t = tf.placeholder(tf.float32, shape=[None, n_out]) n_batch = tf.placeholder(tf.int32) y = inference(x, n_batch, x_len=x_len, n_hidden=n_hidden, n_out=n_out) loss = loss(y, t) train_step = training(loss) correct_pred = tf.equal(tf.argmax(y,1), tf.argmax(t,1)) accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32)) epochs=5000 batch_size=100 init=tf.global_variables_initializer() sess=tf.Session() sess.run(init) n_batchs=N_train//batch_size loss_his=[] for epoch in range(epochs): X_,Y_=shuffle(X_train,Y_train) for i in range(n_batchs): start=i*batch_size end=start+batch_size sess.run(train_step,feed_dict={x:X_[start:end],t:Y_[start:end],n_batch:batch_size}) val_loss=loss.eval(session=sess,feed_dict={x:X_,t:Y_,n_batch:len(X_)}) loss_his.append(val_loss) print (epoch,val_loss,sess.run(accuracy,feed_dict={x:X_train,t:Y_train,n_batch:len(X_)})) print ("Result:",sess.run(accuracy,feed_dict={x:X_validation,t:Y_validation,n_batch:N_validation})) est=sess.run(y,feed_dict={x:X_validation,t:Y_validation,n_batch:N_validation}) np.savetxt("estimated.csv",est,delimiter=",") np.savetxt("Y_validation.csv",Y_validation,delimiter=",") fig=plt.figure() plt.plot(range(len(loss_his)),loss_his,color="red") plt.xlabel("x") plt.ylabel("Loss") plt.show() |
結果
|
1 2 3 4 5 6 7 8 9 10 11 |
4990 0.635243 0.635641 4991 0.637583 0.631736 4992 0.641653 0.62918 4993 0.637389 0.632659 4994 0.641875 0.623855 4995 0.639776 0.629109 4996 0.638922 0.634434 4997 0.641634 0.626411 4998 0.637932 0.633866 4999 0.638583 0.629606 Result: 0.547254 |
結果としては、学習データに対しては正答率60%を超えましたが、評価用データに対しては、54%でした。
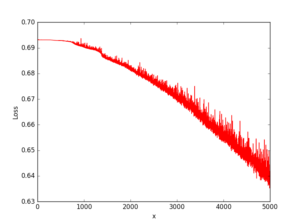
なお、損失関数のグラフは以下の通りとなりました。振動しながら徐々に下がっているような感じです。
ちゃんと学習出来ていると、序盤で一気に下がって、後は殆ど平行状態になるので、
規則性が無いために、オーバーフィッティングになっていると思われます。
なかなか、上手くいきません…
-
前の記事
Pythonでグラフを作成 2017.07.09
-
次の記事

GPU版TensorFlowをWindowsにインストール 2017.07.24